1. Aplicación de los criterios de congruencia y semejanza de triángulos en la resolución de problemas:

la aplicación de los criterios de congruencia y semejanza de triángulos en la resolución de problemas es probablemente uno de los temas más importantes a nivel 3ro de Secundaria,esto es debido a que es necesario identificar ciertas características en figuras geométricas.

antes de empezar a resolver necesitamos saber los criterios de congruencia los cuales son:

a continuación se te proporcionará el link de un video para que fomentes tus conocimientos sobre el tema: https://www.youtube.com/watch?v=XYBOp1uDgAU

al finalizar el análisis de la imagen y el video estas listo para resolver algunos de los ejercicios,¡adelante!:

te recomendamos hacer los ejercicios en papel y después consultar con tu profesor. 

_________________________________________________________________________________

2.Resolución de problemas geométricos mediante el teorema de Tales:

Existen dos teoremas en relación a la geometría clásica,esta recibe el nombre de teorema de tales,ambos atribuidos al matemático griego Tales de Milietino en el siglo VI a.C.

El primero de ellos explica esencialmente una forma de construir un triángulos semejante a uno previamente existente.mientras que en el segundo desentraña una propiedad esencial de los  circuncentros derivados de todos los triángulos reactángulos  que a su vez es utilizado para imponer condiciones de construcción de ángulos rectos,más específicamente expresado como:

toda recta paralela a un lado de un triángulo,forman con los 2 lados o con sus prolongaciones otro triángulo que es semejante al triángulo dado.

a continuación se te proporcionará el link de un video para que fomentes tus conocimientos sobre el tema:  https://www.youtube.com/watch?v=ifjbo-RyfNE

con la información que se te acaba de proporcionar,haz los siguientes ejercicios:

_________________________________________________________________________________

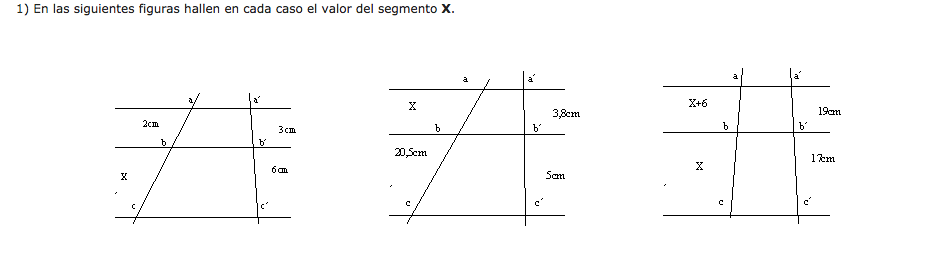
3.Aplicación de la semejanza en la construcción de figuras homotéticas:

Se le llama homotecia a la transformación geométrica que sufre una figura a partir de un determinado punto llamado centro de homotecia.

Al unir los vértices de figuras homotéticas con rectas, éstas se juntan en este punto llamado centro de homotecia (en los ejemplos anteriores y los próximos quedan señalados con la letra O

a continuación se te proporcionará el link de un video para que fomentes tus conocimientos sobre el tema :  https://www.youtube.com/watch?v=PA9DH1PJ9d8

con la información que se te proporcionó resuelve los siguientes ejercicios:

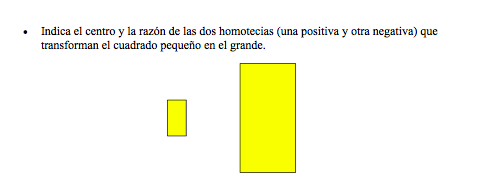
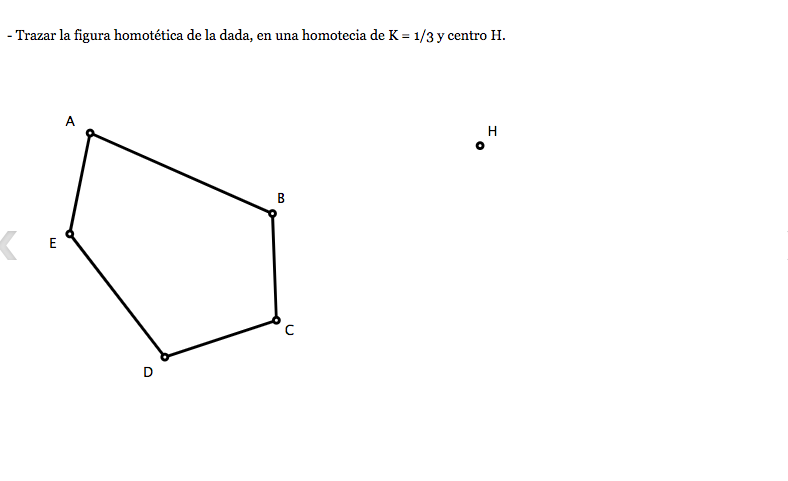
si tienes alguna duda,consulta a tu profesor o averígualo vía internet.

_________________________________________________________________________________

4. Lectura y construcción de gráficas de funciones cuadráticas para modelar diversas situaciones o fenómenos: 

Además de las funciones lineales, uno de los tipos más comunes de funciones polinomiales con las que trabajamos en el álgebra es la función cuadrática. Una función cuadrática es una función que puede ser descrita por una ecuación de la forma y = ax2 + bx + c, donde a ≠ 0. Ningún término en la función polinomial tiene un grado mayor que 2. Las funciones cuadráticas son útiles cuando trabajamos con áreas, y frecuentemente aparecen en problemas de movimiento que implican gravedad o aceleración.

Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:

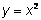La función cuadrática más básica y simple tiene la ecuación . Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática.

a continuación se te proporcionará el link de un video para que fomentes tus conocimientos sobre el tema : https://www.youtube.com/watch?v=gnAdna_tLK0

ejemplo:

_________________________________________________________________________________

 5.Cálculo de la probabilidad de ocurrencia de dos eventos independientes (regla del producto):

"Si multiplicamos o dividimos los dos miembros de la ecuación por el mismo número distinto de cero, obtenemos una ecuación equivalente"

En este caso la regla es igual, pero para multiplicar o dividir por un número que sea distinto de cero.Esta regla la utilizamos para "deshacernos" de los números que multiplican a la incógnita y obtener la ecuación equivalente que nos da la solución.

Por ejemplo, dada la ecuación:

3x=21

Aplicando la regla del producto, dividimos por 3 los dos miembros de la igualdad:

x=7

En general si tenemos  la ecuación:

nº1·x=nº2

Dividimos por nº1 y obtenemos la solución:

x=nº2/nº1

Ahora bien, siempre aplicad primero la regla de la suma y después la regla del producto, por ejemplo, dada la ecuación:

4x-2=18

Primero aplicamos la regla de la suma, sumando 2:

4x=20

Y después la regla del producto,dividiendo por 4:

x=5

Vamos a ver el orden que tenemos que seguir para resolver una ecuación en general.

aquí un video para una mejor comprensión: https://www.youtube.com/watch?v=XPGOa0AE3ZU

_________________________________________________________________________________

6.Obtención de una expresión general cuadrática para definir el enésimo término de una sucesión:

Esto es una ecuación cuadrática: (a, b, y c pueden tener cualquier valor, excepto que a no puede ser 0.) La letra "x" es la variable o incógnita, y las letras a, b y c son los coeficientes Y el nombre cuadrática viene de "cuad" que quiere decir cuadrado, porque el exponente  más grande es un cuadrado (en otras palabras x2). aquí algunos Ejemplos: En esta a=2, b=5 y c=3 aquí un vídeo para ayudar a tu mejor comprensión: https://www.youtube.com/watch?v=4elbNcB3Y0Y ______________________________________________________________________________ 7.Análisis de las características de los cuerpos que se generan al girar sobre un eje, un triángulo rectángulo, un semicírculo y un rectángulo. Construcción de desarrollos planos de conos y cilindros rectos: Es importante prever que los alumnos cuenten con los materiales necesarios (pueden ser otros similares a los propuestos) para realizar esta actividad y alentarlos para que con sus propias palabras describan las características de cada uno de los cuerpos generados: base(s), cara(s) curva(s) y plana(s), altura, generatriz (que corresponde a la hipotenusa del triángulo que lo genera y que no es la altura), cúspide o vértice, radio y diámetro, entre otras. Que concluyan por qué estos cuerpos se conocen como sólidos de revolución. 1. Anticipen qué cuerpo geométrico se describe al girar cada figura. 2. Escriban las características de cada cuerpo generado. Las curvas cónicas: Se llaman curvas cónicas a todas aquellas que se obtienen cortando un cono con un plano. Debido a su origen las curvas cónicas se llaman a veces secciones cónicas. Sin embargo también se pueden obtener algunas de ellas al cortar un cilindro, ¿Qué ocurre en la esfera? a continuación un vídeo: https://www.youtube.com/watch?v=kD5gz2k5IZQ _______________________________________________________________________________ 8.Análisis de las relaciones entre el valor de la pendiente de una recta, el valor del ángulo que se forma con la abscisa y el cociente del cateto opuesto sobre el   cateto adyacente: para el siguiente tema será necesario utilizar solo vídeos por el motivo de que no se ha encontrado otro tipo de información. el valor del ángulo que se forma con la abscisa y el cociente del cateto opuesto sobre el cateto adyacente. Intención didáctica: Que los estudiantes, a partir de la gráfica de una recta, identifiquen a la pendiente como la razón de los catetos de los triángulos rectángulos construidos con la recta y el eje de las abscisas. Consigna: Organizados en binas, y a partir de la gráfica de la recta y = 0.5 x + 1, realicen lo que se pide: consideren las rectas de la siguiente ilustración, las cuales forman con el eje horizontal un ángulo de 30°, uno de 45° y otro de 60°; para formar tres triángulos rectángulos, uno para cada ángulo, posteriormente completen la tabla y contesten las preguntas. Pueden utilizar un juego de geometría y una calculadora. Ángulo: Medida del cateto opuesto: Medida del cateto adyacente: En este caso, se espera que los alumnos puedan determinar que los cocientes de las razones formadas por el cateto opuesto entre el cateto adyacente es 0.5 de cualquier triángulo rectángulo formado entre la recta y el eje de las abscisas. Es muy probable que los alumnos dibujen diferentes triángulos semejantes aquí un vídeo:https://www.youtube.com/watch?v=A6Vp18ctfWc _______________________________________________________________________________ 9.Análisis de las relaciones entre los ángulos agudos y los cocientes entre los lados de un triángulo rectángulo: La utilización de las llamadas funciones trigonométricas data de la época de la antigua Babilonia. 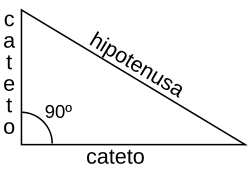Los principios de esta rama matemáticas fuerón desarrollados en su mayoría por estudios de la India, antigua grecia y matemáticos musulmanes.Las funciones trigonométricas surgen al estudiar el triángulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos cualesquiera de sus lados dependen únicamente del valor de los ángulos del triángulo La denominación de los lados de un triángulo rectángulo son las siguientes:* La hipotenusa (h) corresponde al lado que se encuentra opuesto al ángulo recto. * El cateto opuesto (a) corresponde al lado opuesto al ángulo que se quiere establecer. * El cateto adyacente (b) corresponde al lado que es adyacente al ángulo que se busca establecer. razones trigonometricas: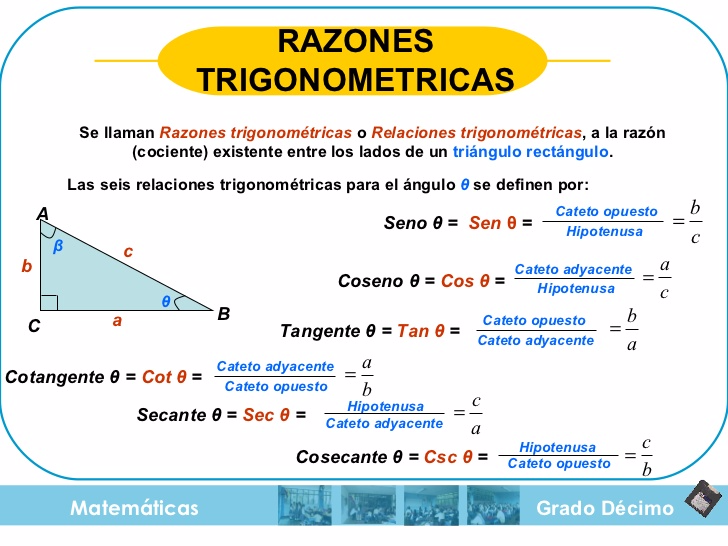 aquí un video: https://www.youtube.com/watch?v=6BwYdQJrjsM _______________________________________________________________________________ 10. Explicación y uso de las razones trigonométricas seno, coseno y tangente. Seno, coseno y tangente Las tres funciones más importantes en trigonometría son el seno, el coseno y la tangente. Cada una es la longitud de un lado dividida entre la longitud de otro... ¡sólo tienes que aprenderte qué lados son! Para el ángulo θ : Función seno: sin(θ) = Opuesto / Hipotenusa Función coseno: cos(θ) = Adyacente / Hipotenusa Función tangente: tan(θ) = Opuesto / Adyacente Nota: el seno se suele denotar sin() (por la palabra inglesa "sine") o sen(). Aquí utilizaremos sin() pero puedes encontrarte la otra notación en otros libros o sitios web. Sohcahtoa Sohca...¿qué? ¡Sólo es una manera de recordar qué lados se dividen! Así: Soh... Seno = Opuesto / Hipotenusa ...cah... Coseno = Adyacente / Hipotenusa ...toa Tangente = Opuesto / Adyacente ejemplo: vídeo: https://www.youtube.com/watch?v=mf6EKunOnzw _______________________________________________________________________________ 11.Cálculo y análisis de la razón de cambio de un proceso o fenómeno que se modela con una función lineal. Identificación de la relación entre dicha razón y la inclinación o pendiente de la recta que representa. Cálculo y análisis de la razón de cambio de un proceso o fenómeno que se modela con una función lineal. Identificación de la relación entre dicha razón y la inclinación o pendiente de la recta que la representa. obtengan, a partir de la gráfica de una función lineal, las razones de cambio del fenómeno que representa. analicen la siguiente gráfica que muestra los cambios en el precio de un artículo durante los primeros meses del año, posteriormente den respuesta a las preguntas. ejemplo:

vídeo:  https://www.youtube.com/watch?v=xQ-e5pMaNOg

________________________________________________________________________________

Último tema:Medición de la dispersión de un conjunto de datos mediante el promedio de las distancias de cada dado a la media 

as medidas de dispersión nos indican que tan lejos pueden quedar los datos de lo normal, es decir del centro de la distribución de los datos.

Rango

En matemáticas y estadística, el Rango es la diferencia existente entre el valor mayor y el menor de la distribución. Lo notaremos como R. Realmente no es una medida muy significativa en la mayoría de los casos, pero indudablemente es muy fácil de calcular.

R=Vmax – Vmin

Es decir esta medida nos dá el rango o tamaño de la distribución.

Desviación Medía

En el ámbito de la estadística, la desviación media es la media (promedio) de las diferencias en valor absoluto de los valores a la media. Para esto debemos entender que es la desviación, esta es la diferencia entre la Media y un valor tomado. Posteriormente se toman estas diferencias, se determinan los valores absolutos de cada una, se suman y se dividen entre el número de todas. Si se llegase a determinar el promedio de las desviaciones sin obtener primero el valor absoluto, se obtendría en la suma Cero.

Varianza

 

En Teoría de Estadística, la varianza es una medida de su dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media. Está medida en unidades distintas de las de la variable. Por ejemplo, si la variable mide una distancia en metros, la varianza se expresa en metros al cuadrado. La desviación estándar, la raíz cuadrada de la varianza, es una medida de dispersión alternativa expresada en las mismas unidades. La varianza tiene como valor mínimo 0. Hay que tener en cuenta que la varianza puede verse muy influida por los valores atípicos y no se aconseja su uso cuando las distribuciones de las variables aleatorias tienen colas pesadas. En tales casos se recomienda el uso de otras medidas de dispersión más robustas. El término varianza fue acuñado por Ronald Fisher en un artículo de 1918 titulado The Correlation Between Relatives on the Supposition of Mendelian Inheritance.

Desviación Estándar o Típica

Es una medida de centralización o dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva. Se define como la raíz cuadrada de la varianza. Junto con este valor, la desviación típica es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.

créditos de la información a quien corresponda.